Unveiling the Harmonies of Nature: Scientific origins of the Apollonian
The following short argument represents an initial enquiry into the physical origins of what we, as human beings, perceive as ordered, harmonious, and beautiful. Using the nomenclature of Nietzsche – Apollonian. This short article was originally embedded in a longer piece on the Apollonian vs Dionysian forces in art, specifically in the works of Rembrandt. Readers can find an introduction to these concepts in the introduction to that article. Hopefully however, this revised piece is able to stand alone and make sense as an individual thought.
“In short, Apollonian denotes harmony, structure, order, and light. Whereas Dionysian denotes chaos, fertility, emotion, and the dissolution of boundaries.”
First, we shall take a look at the structure of these two forces and where they sit in relation to one another. I argue that the Dionysian is constant and runs underneath the Apollonian. The analogy with Rembrandt’s paintings is that the Dionysian is manifest in the seemingly disordered brush work when examined up close; whereas the Apollonian is manifest from a distance in the harmonious arrangement of shape and form.
A scientifically motivated analogy here is that between Quantum and Newtonian mechanics. At the quantum level, nature itself is inherently uncertain. It is not possible to know the exact location and momentum of a particle for example (Heisenberg’s principle of uncertainty). Nor is the nature of a quantum mechanical state known until it is observed or measured – that is, it interacts with another state. The principle of superposition posits that the wavefunction* exists in a superposition of an infinite number of possible states, each with an associated probability, until it is measured. When measured, the state collapses into a single measurable state. Therefore, the world of quantum mechanics, and thus the universe, truly has uncertainty embedded at its very heart. It is certainly counterintuitive, yet it is real. Or, at the very least, it does a remarkable job of describing the physical laws of the universe at the smallest length scales, to within an experimentally measured accuracy that should rule out the idea that the entire theory is simply a coincidence.
However, when large numbers of quantum states are brought together – in molecules, groups of molecules and then eventually the macroscopic objects you can see and touch, the ensemble observation is one of Newtonian properties. It is possible to know the position and momentum of an object at this scale. It is equally impossible that an object exists in an infinite number of superpositioned states at any given time – the table in front of you remains as a table and its behaviour in time and space abides strictly by analytical/mathematical expressions of Newtonian motion. The analogy I’m trying to draw with this slight digression is that reality is not consistent at every level of observation. Whether that be a level of observation, judgement, or “will”. What often manifests as stable, ordered, and predictable at the larger scales, in reality has a complex and unpredictable structure beneath. As I argue is pertinent to giving the “life” to Rembrandt’s paintings.
*The wavefunction in quantum mechanics can be understood as a mathematical description that captures the behaviour and properties of a quantum system, such as an electron or a photon. It provides information about the probabilities of different outcomes when measuring certain properties of the system.
The principle of correspondence: Mathematical truths - the real world foundation of the Apollonian?
An exception to this, is perhaps offered by the principle of correspondence. In physics, this posits that although weird at the quantum mechanical level, the laws of physics cannot be inherently “different” to another level. In practice, this is followed by taking macroscopic limits of quantum mechanical equations (for example summing over an infinite number of particles or states rather than only one or two). When such a limit is taken, the equation must be equivalent to the macroscopic equations of physics such as the corresponding Newtonian laws of motion. Engrained in this principle however, is what happens when mathematical laws are already the same at the level of quantum mechanics, as well as the level of our macroscopic world? For example, the behaviour of waves. At the level of quantum mechanics, particles are described by wavefunctions, which are mathematical representations of their state. Everything that can be known about a particle is encoded in its wavefunction – for example, the probability of finding a particle in different states or positions. I won’t delve too deeply into wave-particle duality here, but the short point I would like to make is that the particles at one of the smallest levels of nature, fundamental particles such as electrons, quarks, and so on, due to the formulation of their wavefunctions can in many instances be observed to behave as waves (as the name wavefunction might suggest). In fact, the equations that describe their behaviour are the same in form as those used to describe other (macroscopic) forms of wave – such as acoustic waves (sound). When two or more quantum states combine, their wavefunctions can interfere constructively or destructively – this can lead to characteristic interference patterns observed in experiments such as passing these particles through gratings. Now, not all of the physics is the same and it would be naïve to draw a one-to-one correlation between quantum waves and the waves in the ocean – yet the principles such as wavelength, frequency, and wavenumber remain.
Geometric patterns, whether manifested in the resonances of auditory waves, the morphology of botanical entities, the intricacies inherent in our genetic blueprint, or the trajectories traced by celestial bodies, seemingly adhere to the unifying tenets of Toroidal Geometry. It is within this geometric framework that the profound interplay of mathematical and spatial principles becomes apparent, thus elucidating the enigmatic phenomena of cymatic configurations, as exemplified in the image provided above.
Spanning the immeasurable reaches of the cosmos, every form and configuration conforms steadfastly to the immutable laws of vibration and frequency. These universal laws, deeply entrenched within the realms of vibrational dynamics and cyclical occurrences, serve as the foundational bedrock for the fundamental principle commonly referred to as the "Law of Correspondence." This principle, acting as a beacon of insight, offers a coherent explanation for the pervasive presence of self-resemblance and fractal properties observed ubiquitously throughout the tapestry of existence, spanning from the infinitesimally minute to the grand tapestry of the macrocosmic dimensions. From the subatomic realms to the resplendent galactic expanses, the vast symphony of the cosmos reverberates in consonance with the harmonious dictates of the Law of Vibration.
The reason for introducing this admittedly quite technical digression in the discussion of the Apollonian and Dionysian concepts, is that it brings about an interesting question. Universally, what does it mean to be structured and harmonious, and where do these concepts really come from? It requires, I believe, an entity that holds no matter what level of reality it is observed in. In this case, I have highlighted one – waves and resonance.
The celestial spheres
An ancient theory of Pythagoras and Aristotle proposes a universal cosmology which described the universe in terms of spheres. In this theory, the celestial entities were pinned to the spheres and their motion driven by something like musical sound. The Greeks realised that spherically shaped amphoras, with an opening of a specific size and shape, when placed in flowing air would generate beautiful “harmonious” sounds. What they had discovered was indeed musical harmony and natural frequencies. Place two amphoras next to one another with their relative sizes generating frequencies at a 3:2 ratio and you generate a perfect fifth. The perfect fifth sounds stable and “right” – not arbitrarily, but because in the fundamental laws of wave equations, it actually is. Place two next to another with their shapes generating frequencies at a 2:1 ratio and you have an octave, and so on.
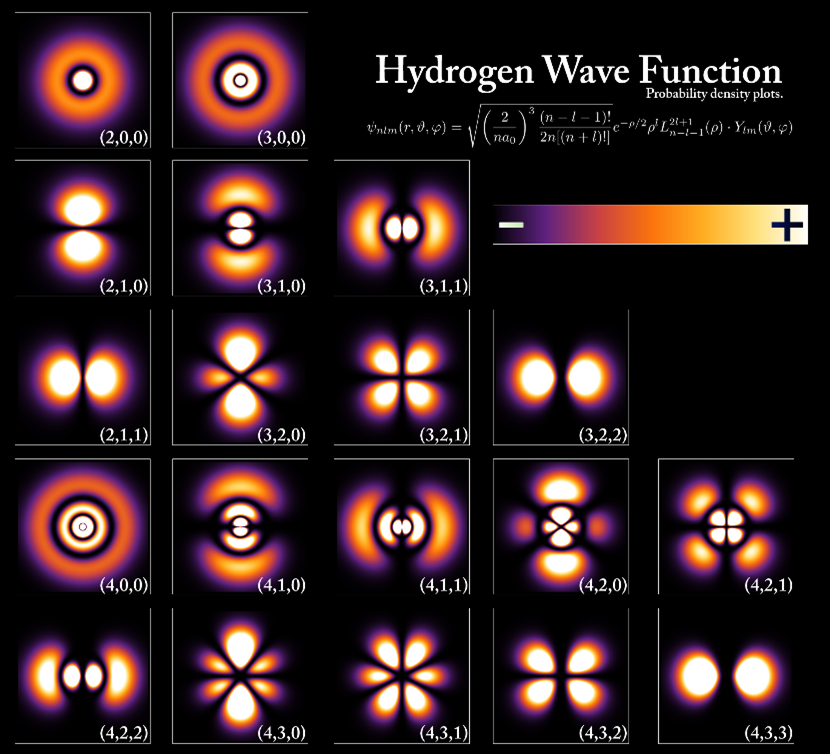
(Left): A real world (not just abstract mathematical) manifestation of the wave-like behaviour of particles and matter. The wavefunction of the atomic orbitals of the atom hydrogen at increasingly higher energies. What emerges are elegant, beautiful geometrical patterns. (Centre): The pattern that emerges when a particle is trapped inside a two dimensional box. Due to behaving like a wave, a particle’s wavefunction interferes constructively and destructively at integer and fractional integer positions along the edge of the box – exactly the same as a string on a guitar. (Right): Beauty in music. The waves of the fundamental pitch (blue) the perfect fifth (green) and first harmonic (octave – orange). Is the reason why we perceive the relationship between these pitches in our ear as stable and beautiful due to the fact that they are mathematically within perfect ratios of one another?
This runs quite deep and will require an entirely separate body of work to do it justice. I do not want to distract too much to the main thoughts of the previous article on the Apollonian and Dionysian concepts in Rembrandt, but I think the concept is certainly worth mentioning – as it takes the idea of Apollonian order/harmony and begins to provide an actual foundation for what that otherwise nebulous concept is and where it could conceivably originate.
Furthermore, I encourage you, the reader, to keep these ideas in mind when in the other article I will reference another purely mathematical construct – the golden ratio – which again has founding in the physical laws of the universe. Not at this stage to understand the concept entirely, but to spark interesting thoughts for another time linking what we perceive as beautiful and right to the world of physics and mathematics.