An introduction to semiconductor physics
The publishing embargo has recently been lifted on my PhD thesis, which means that the work is now available in the public domain.
You can access the full document through the University of Cambridge repository here.
Much of the thesis, as you might expect, describes the specific research and data undertaken during the PhD - which although interesting to the scientific community, doesn’t lend itself well to general interested reader.
Some chapters, however, were written to provide the audience with a warm introduction to the general principles that underpin much of the work. This is particularly the case for some early chapters on semiconductor theory.
I therefore provide a copy of this specific chapter here for anybody who might be interested in learning about this fascinating class of materials - which arguably underpin most of modern life. The work is targeted at those with a basic background in quantum mechanics and physics. However, the content is still very much accessible to those without this training and the text should still make sense, even if much of the mathematics is skipped over.
The link above will give you a pdf of the chapter - which as many of you will know is a far smoother way of integrating scientific equations into text (websites are not great for this). However, for those of you that wish to remain on the website, an online-friendly version is provided below.
Enjoy!
Introduction
Semiconductor theory
The study of solid state physics and shortly thereafter semiconductors began after the early work regarding the X-ray diffraction of crystalline materials. Indeed, it is the periodic array of atoms within crystalline materials that gives rise to both the characteristic reflections from X-ray diffraction and the energy bands that ultimately give them their semiconducting properties. As opposed to non-crystalline solids, which typically have neither [26].
In short, many of the interesting and distinguishing properties of crystalline materials comes from the interplay between the electron wave functions and the periodic arrangement of the atoms in the material. In a crystalline material, the wavelength of the electron is short and therefore highly responsive to the local periodic arrangement of the atomic potentials. Whereas in a non-crystalline material, the electron-lattice interaction is significantly dimin- ished. Somewhere between the two, in glasses for example, the wavelengths of light are long enough that they interact with an average order in the materials over much longer length scales, that the electron wavefunctions cannot.
A semiconductor is a class of crystalline material that exhibits electronic properties, somewhat eponymously, between a conductor and an insulator. This is due to the size of the energy band gap, to be described shortly, which typically sits at approximately 0.25 to 2.5 eV and separates the valence and conduction band electrons. Owing to this fine balancing of the conductivity of the material, it can be altered dramatically by relatively small inputs such as temperature, illumination, magnetic fields and the incorporation of extrinsic impurity atoms. Having such a fine control over the electronic properties of a material, that can also be manufactured into complex and microscopic devices, has given rise to the remarkable versatility and widespread adoption of semiconductors in all but few aspects of modern life. It is quite staggering how dramatically the human condition has transformed, between the first demonstration of the transistor by John Bardeen, Walter H. Brattain, and William B. Shockley at the Bell Labs in 1947 [27] and today. It is almost impossible now to imagine a world, particularly in a developed nation where computers, mobile phones, LED lighting, electronic displays and the internet do not exist. At their very heart, all of these technologies run on semiconductor platforms. Perhaps in the same sense that the last technological revolution was posthumously named the "steam" or "industrial" revolution, the period during which this thesis is written could well be named the "semiconductor" or "information" revolution by generations of historians to come. Where information itself no longer resides in books, poems, or myth, but in series of 0s and 1s, written by a semiconductor into another semiconductor to be read out later by another semiconductor and thence displayed by a light-emitting semiconductor! It is as though as a global society, we are slowly creating a new form of collective consciousness - this time residing in the electrons of inorganic semiconducting materials.
Traditional semiconductors are inorganic crystalline materials residing mostly in column IV of the periodic table, silicon (Si), germanium (Ge) and in column VI, selenium (Se) and tellurium (Te). Additionally, there are the inorganic compound semiconductors such as gallium arsenide (GaAs), which is a combination of the column III gallium and column V arsenic. The following sections on semiconductor theory will be written with these pure materials in mind, as they demonstrate neatly the periodic arrangement of atoms in a crystal structure that gives rise to semiconducting properties. However, as will be shown later, the main class of semiconducting materials used in this thesis is the organic-inorganic hybrid sub-class - metal halide perovskites. Despite variations in the type and arrangement of atoms and bonds in these materials, the defining properties however are universal. There exist also materials that demonstrate semiconducting properties that are entirely organic, due to the overlap of molecular orbitals giving rise to a similar energy structure to the overlap of atomic orbitals described shortly. These will be touched upon later when discussing the use of electrochemical doping techniques.
Band theory of semiconductors
There exist many options with which to derive the general properties of semiconductors, starting with the most basic quantum mechanical assumptions. Each text book and teacher will have their own subtly nuanced way of navigating the subject. The following approach is based on a combination of the approaches of Charles Kittel in "Introduction to Solid State Physics" [28] and that of B.H. Bransden and C. J. Joachain in "Quantum Mechanics" [29]. I have found such a presentation and chronology of the subject to provide an effective framework in various talks and undergraduate supervisions that I have given.
The atomic lattice
The easiest way to build a theory of semiconductors is to do just that - start with a collection of atoms and build a semiconductor right on the page as it were. This is done by arranging atoms (specifically atomic potentials) mathematically in a periodic arrangement. Once the atomic arrangement comprising the solid state material has been described, it is then possible to investigate the behaviour of electrons in the resulting arrangement and understand the properties that emerge.
A crystal, by definition is comprised a perfectly periodic arrangement of atoms. This can be described by attaching atoms to a vector basis that for any position r, will look identical if translated and looked at from position r′ thus,
r′ = r+u1a1 +u2a2 +u3a3 (2.1)
where u1, u2 and u3 are arbitrary integers and a1, a2, a3 are three translational vectors defining the space lattice. The basis of a crystal structure is then simply an atom, or group of atoms, to be placed at each of these lattice points in space as shown in Figure 2.1.
Figure 2.1 Building a crystal structure - the space lattice and the basis. (a) The space lattice defines repeating points in space. (b) An arbitrary basis formed by two different atomic species. (c) The crystal structure created when the basis is applied to each point on the space lattice.
By extending the space lattice into three dimensions, all known solid crystal structures may be described by the appropriate lattice symmetry and atomic basis. To cover all possible symmetry operations, rotations and mirror reflections, a total of five distinct lattice types must exist in 2 dimensions - these are the five Bravais lattices. To extend the point symmetry groups into 3 dimensions, a total of fourteen lattice types must be used to describe all possible symmetry restrictions. These are grouped into seven categories according to the geometries of the unit cell, and are described in Table 2.1. The relative lengths of the unit cell vectors and angles between them (α, β, γ) are indicated accordingly.
These 3D lattice types will be revisited when the crystal structure of the metal halide perovskites during lithium ion insertion is discussed. For now, they serve as an illustrative guide and one has to imagine an atomic basis stamped in 3D space at each point described by these space lattices.
Table 2.1 The seven categories of crystal lattice in three dimensions. Each category has a corresponding set of sublattices. The restrictions on the unit cell lengths and relative angles for each category are indicated.
Emergence of the bandgap
Semiconductors are fundamentally defined by the gap that exists between the valence and conduction energy bands in the material. In this section, the periodic crystal lattice described above will be treated quantum mechanically and in doing so, the splitting of electron energy bands within the material will be demonstrated.
To begin with, I will consider the simplest case in one dimension (x), in which there is a constant potential V (x) = V0. The time dependent Schrödinger equation in one dimension is,
where ψ represents the wavefunction of the system - in this case, an electron; and m its mass. If the spatial components are packaged up into a single operator, the Hamiltonian, which describes the total energy of the system when it acts on the wavefunction,
Generalisation from one dimension along x to three dimensions along r is trivial and
simply requires that the differential with respect to x is replaced by the Laplacian operator. If the potential V is time-independent, it is possible to separate the time and spatial variables such that both the time dependent side of the equation and time independent side must be equal to a constant. We can call this constant E. Solving the time independent side, having equated the time-dependant simply to E,
where E therefore describes the energy of the wavefunction ψ . E here has no time dependence and remains constant. The form of Equation 2.7 is that of a stationary state (constant energy) describing a free particle of momentum p and definite energy E = p^2/2m. In order that probability is maintained, the solutions (wavefunctions) must be continuous, finite and single valued. The first derivative with respect to x must also be continuous and smoothly varying.
Most undergraduate text books will typically at this stage run through the many examples of solving the time independent Schrödinger equation for a set of known scenarios. Such as; a potential step which represents the scattering of a particle off a point; a potential barrier which represents a boundary between two materials; infinite square wells which demonstrate the quantisation of the wavefunction; and, finite square wells which represent a more physical example of the potential environment around an atom. Solving the Schrödinger equation for each of these scenarios introduces a priori the notion of tunnelling, reflection off a barrier of lower energy than the particle, and the quantisation of energy and momentum. Which although breathtaking, the derivation of all will unnecessarily dilute the contents of this thesis. For full discussions of each of these scenarios see textbooks by Griffiths [30] and Bransden & Jochain [29]. For the purpose of this thesis, I will only consider the scenario which demonstrates from first principles where the energy gap in a semiconductor originates - a series of periodic potential wells of finite potential.
Figure 2.2 The finite potential well. The wavefunction of the electron is confined into a two-dimensional well of width a and walls of potential energy E = V0, where V0 is finite. Standing waves within the well are observed and quantum tunnelling results in a small portion of exponentially decaying wavefunction to be present in classically forbidden regions outside of the well. The first three solutions to the Schrödinger equation are shown.
In order to do so, first consider a single finite potential well in isolation. A finite potential well, consists of a ‘well’ of width a and walls of potential energy V0 as shown in Figure. 2.2. In order to describe this system completely, the Schrödinger equation must be solved for each region in space. This includes the region to the left of the well (Region I), inside the well itself (Region II) and to the right hand side of the well (Region III). Inserting the value for the potential in each of these regions into the Schrödinger equation gives the following set of equations to be solved,
where k1 = k3 = p2m(V0 − E )/ħ2 and k2 = p2mE /ħ2 describe the wave numbers of the solutions in each of the three regions (k = 2π/λ). A1,A2,B2, and A3 are normalisation constants, which are necessary to maintain probability. These solutions describe wavefunctions of exponential decay in the Regions I and III - classically forbidden regions. This incidentally is the quantum tunnelling phenomena of the wavefunction through a finite potential barrier. Within the well itself the solutions are sinusoidally varying wavefunctions of discrete energies that resemble standing waves. The energy values are quantised by the quantum number n, meaning that the electron wavefunctions have only discrete values of wavelength, λn.
In order to extend this abstract example to what happens in a crystal material, it is necessary to introduce multiple finite potential wells in close proximity to one another, to model the bringing together of multiple atoms. Note that in reality, atomic potentials are not exactly described by square wells, but the results are in a general sense the same. Essential to the description of a crystalline material and therefore a traditional semiconductor, is the requirement that the atoms are arranged in a periodic lattice. That is, a potential V such that,
where l is the periodic distance between two potential wells, shown in Figure 2.3 where l = a + b. This arrangement of finite potential wells is known as the Kronig-Penney potential and is a reasonable description of the interactions to which an electron is subject in a crystal material.
Figure 2.3 The periodic finite square potential. Modelling the atomic arrangement in a crystalline material. An infinite number of 2 dimensional finite potential wells of width a are assembled a distance b apart. The potential barrier between each well is defined with energy E = V0 = 0 such that the energy within the wells is negative.
Floquet’s theorem
Due to the symmetry of the periodic potential, it is required that if ψ(x) is a solution to the Schrödinger equation at x corresponding to energy E, then ψ(x+l) must also be a solution. Furthermore, due to being a second order linear equation, any solution may be represented by a linear combination of two independent solutions. That is, if ψ1(x) and ψ2(x) are both solutions to the equation, then so is ψ3(x) = c1ψ1(x) + c2ψ2(x), where c1 and c2 are normalisation constants. Therefore, since ψ1(x + l) and ψ2(x + l) are solutions to the Schrödinger equation, so too must be their linear combination. Solving for the three equations that result, considering the normalisation constants in the eigenvector/eigenvalue matrix, two solutions have the following form,
where K corresponds to the reciprocal lattice vector and is a real value. Since e^(ni2π) = 1 (n is an integer), a complete set of wavefunctions may be obtained from defining and limiting the value K to between,
Bloch’s theorem
where ψ(x) describes the Bloch wavefunction and uK(x+l) = uK(x), the periodic amplitude. Bloch’s theorem therefore describes a wavefunction that is a travelling wave, of wavelength 2π/K, with a periodic amplitude uK(x) that varies with the same periodicity, l, as the periodic potential - the crystal lattice. A beautifully neat solution, to which F. Bloch himself commented,
“When I started to think about it, I felt that the main problem was to explain how the electrons could sneak by all the ions in a metal... I found to my delight that the wave differed from the plane wave of free electrons only by a periodic modulation!”
Thus far, it has been shown that solutions to the Schrödinger equation for a periodic potential have the general form described by a Bloch wave in 2.19. From this it is inferred that any given electron does not necessarily belong to any given atom or ion in the lattice, but has a certain probability of being found with any neighbouring atom. In the case of a free electron, described by the wavefunction in Equation 2.7, when V0 → 0, the allowed energy states of the electron are described by,
that is, a parabolic dispersion of energy with a given wave number k, which is related directly to the wave momentum by the de Broglie relation p = ħk. This E-k relationship is shown in Figure 2.5 (a). This description is reasonably accurate for a metal, where the interaction between the periodic arrangement of central ions and the sea of electrons is relatively weak, i.e. free electrons. The fact that electrons in such a structure somewhat behave as free particles/waves goes some way to describe the conductive nature of most metals. However, in the case of a semiconductor, the interaction between the periodic potential (described by the Kronig-Penney potential in this model) is stronger, resulting in Bragg reflections and the emergence of forbidden energy states.
Considering the allowed values of momentum, k, in the crystal lattice - i.e. in reciprocal space, the periodicity of the potential is such that the wavefunction, and therefore k, is indistinguishable from the wavemomentum k + 2πl/a. Therefore it makes little sense to describe an infinite number of wavefunctions throughout the crystal and it is only necessary to describe the wavefunctions within the first region, after which they all repeat. This region is called the first Brillouin zone and describes momenta between −π/a ≤ k ≤ π/a. At boundaries between these Brillouin zones, a portion of the wavefunction will be reflected, if the interaction between the periodic potential and electron wavefunction is significant enough, when the following is satisfied,
describing a standing wave comprising left-travelling and right-travelling waves in equal parts. The standing waves ψ(+) and ψ(−) pile up electron density at different regions within the periodic lattice, as shown schematically in Figure 2.6.
Magnitude of the energy gap
This demonstrates how the magnitude of the energy gap between the two bands is proportional to the Fourier component of the periodic potential. This makes sense given the fact that the standing waves with ψ(+) have a higher probability density at the positions of the nuclei, and standing waves with ψ(−) have a higher probability density in the space between nuclei, as shown in Figure 2.6. Due to this distance, ψ(−) must have a higher potential energy than ψ(+) at the Brillouin zone boundary (at k = ±π/a). If the average value of the potential energy forming from the accumulated electrons is calculated, it is found that the potential energy from ψ(+) is lower than that of the travelling wave. Conversely, it is found that the potential energy from ψ(−) is higher - with the difference between the two being equal to EG. This bandgap is shown in the modified energy E − k dispersion relation for a "nearly free" electron in Figure 2.5 (b), at edges of the Brillouin zone.
As the atomic potentials are brought closer together, the strength of their interactions increases. As such, many right and left travelling waves build up and result in an increasingly complex structure of available energy levels. Once this reaches a certain point, when the levels are so high in number and close in energy - the possible selection of states available for an electron to occupy effectively becomes continuous in energy. This gives rise to the term energy band rather than simply energy level. This is shown schematically in Figure 2.7. As the separation between potentials becomes smaller, continuous bands form. Conversely, in the limit that they become infinitely separated, discrete energy levels as in the original isolated finite well are recovered.
Effective mass
The lower of the energy bands described above is called the valence band and the higher the conduction band. Electrons in the valence band are located within the vicinity of the atomic cores, whereas electrons excited to the higher energy state are free to propagate through the lattice - conduction electrons. By taking the Taylor series expansion of E(k) around the conduction and valence band edges, it is found that,
where the positive and negative results correspond to the conduction and valence bands respectively and m∗ corresponds to the effective mass of the electrons in the material. The effective mass accounts for the difficulty to move electrons within the material, given the strength of their interaction with the periodic potential. For example, in a metal the electrons will have a relatively low effective mass since the application of a small electric field will result in the rapid acceleration of the electrons. Conversely, in a material with a strong electron potential coupling, the electrons will respond sluggishly to the external field - as though they have a much higher mass. By rearranging Equation 2.27 it can be seen that the effective mass depends on the curvature of the energy bands.
Occupation of bands and density of states
Now that the band structure description of semiconductors has been achieved, it is important when looking at the electronic and optical properties of a material, to understand how each energy state may be occupied by the electrons in the system.
It was remarkable to note in the previous section how conduction electrons are able to move so freely through a condensed matter system - whether it be the free electrons in a metal, or the conduction band electrons in a semiconductor. We saw how this was due to the fact that the waves describing the electrons (Bloch waves) can propagate freely through a periodic arrangement of atoms/ions. This leaves only the scattering between one electron and another to impede an electron’s progress through space. This is effectively a result of the Pauli exclusion principle which prevents two electrons from simultaneously occupying the same state. A consequence that follows from the same principle arises when considering how electrons occupy a condensed matter system, when electrons are added in one by one, starting with the lowest energy first. If we consider adding N electrons into the system (and for simplicity’s sake let N be even), then we may define nF as the value of n which occupies the highest energy state. The Fermi energy, EF then describes the energy of this state in one dimension thus,
where L is the length of the 1-dimensional line to which the states are confined. At finite temperature, the system becomes slightly more complex since states that were otherwise empty have a probability of becoming filled; conversely states that were otherwise filled now have a probability of becoming vacant. The probability that a state of energy E will be occupied at a finite temperature T follows the Fermi-Dirac distribution,
where μ is the chemical potential of the system - the energy required to add or remove an electron at a given temperature, and kB the Boltzmann constant. It follows that at absolute zero, the chemical potential is equal to the Fermi energy, since the highest occupied state must by definition be at the Fermi level. Under the Boltzmann approximation, for an intrinsic semiconductor (see the following section for a discussion on the case of an extrinsic semiconductor), it is shown that the chemical potential of an intrinsic system is,
i.e. it lies approximately at the centre of the bandgap (Eg/2). Combining this result with the Fermi-Dirac distribution, we can deduce the occupation of the conduction band at a given temperature T as,
where NCB, NVB are the effective density of states for the conduction and valence bands. From this, we find that the intrinsic charge carrier density of a semiconductor ni is an inherent property of a material and is given by,
n= p=ni (2.25)
where n is the electron charge carrier concentration and p the hole concentration. In a lightly doped semiconductor the relation between the charge carrier concentrations becomes,
n0 · p0 = n2i (2.36)
From this, it is deduced that for an intrinsic semiconductor, the product of the number of electrons and holes is at a constant state of equilibrium and depends only upon the temperature and bandgap EG of the material. We shall see in subsequent sections how this changes when extrinsic semiconductors are formed by the intentional addition of external species, which add or remove electrons from the lattice (doping).
Doping
On their own, the potential applications of semiconductors are somewhat limited. How- ever, through the addition of external species (atoms, ions, impurities, defects etc.) into the semiconductor lattice, the properties of semiconductors can be tailored, giving rise to a plethora of devices and material configurations. In this section, conventional doping theory and approaches will be introduced such that a foundation can be formed, upon which the interpretation of doping in halide perovskites can be built.
Doping in semiconductors takes two forms: n-type and p-type doping. n-type doping involves the introduction of additional negative charge carriers into the semiconductor and p-type the removal of negative charge carriers, or equivalently the addition of a hole. This is achieved by intentionally adding impurities into the structure that either donate an electron or remove one. In an intrinsic semiconductor, that is a pure semiconductor with no doping, the concentrations of holes and electrons as described by Equation 2.35 are equal under thermal equilibrium, with the chemical potential sitting approximately at the centre of the bandgap.
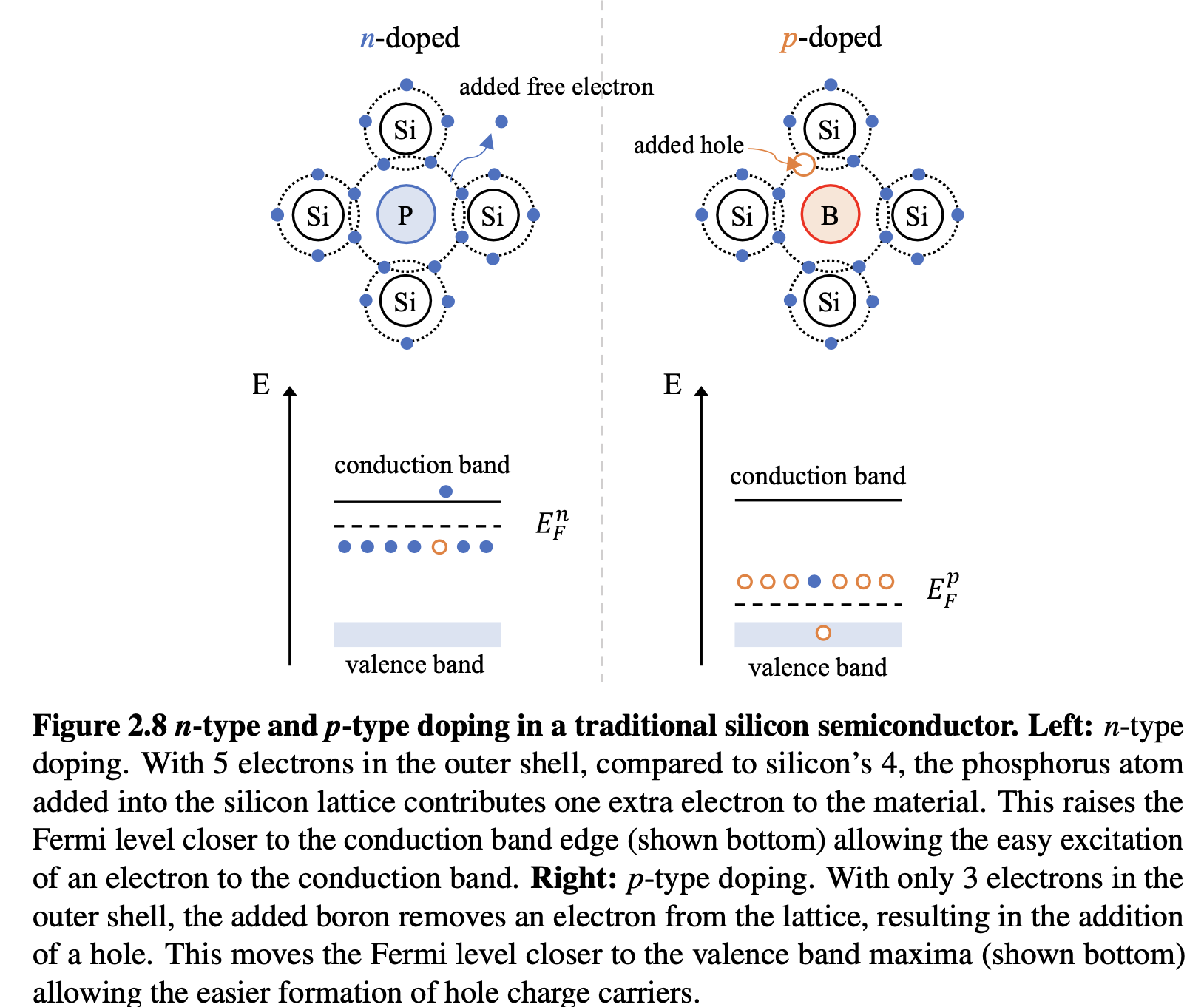
A simple doping method to consider first is the substitution technique. By changing an atom in the semiconductor lattice for one with an additional electron in the outer shell, n-type doping can be achieved due to the easy excitation of this additional electron, which is not strongly coordinated to any particular bond. In silicon for example, phosphorus which has 5 electrons in the outer shell compared to silicon’s 4, can do exactly that - as shown schematically in Figure 2.8. Boron on the other hand has only 3 electrons in the outer shell and will therefore draw an electron from the silicon lattice, thus resulting in a hole in the valence band - p doping the material. This is shown on the right hand side of Figure 2.8. The ensuing effect is the introduction of allowed energy states within the bandgap of the silicon at energies very close to the conduction band (for n-type) and valence band (for p-type).
Consider first the effects of introducing an electron donor impurity to the semiconductor (phosphorus to silicon). At very low temperatures T → 0K, the donor levels just below the conduction band are partially occupied and thus, the chemical potential is near the donor level and n ≫ p. Then as T is increased, most, if not all of the donor levels are ionised to the conduction band and the chemical potential sits just below the conduction band - as shown bottom left in Figure 2.8. Conversely, at finite temperatures, in the case of p-doping, the added available states just above the valence band result in electrons being excited from the valence band to the acceptor state (EFp), leaving hole states behind in the valence band as shown in the bottom right of Figure 2.8.
Generally speaking, increasing doping levels result in increased conductivity in a semi- conductor, due to the consequent increase in the charge carrier concentration. Indeed, semiconductors that undergo high levels of doping become degenerate and exhibit con- ductivities closer to that of a metal than a semiconductor and one which increases with temperature.
Construction of p-n junctions
Above, the effect of doping in a single "piece" of semiconductor is considered. However, almost all semiconductor technologies - such as solar cells, LEDs and transistors come not from a single n- or p-type material, but the mating of the two. Since the Fermi level in a material must remain constant at thermodynamic equilibrium, the bringing together of a n-type and p-type semiconductor must result in some rearrangement of the energy bands at the interface such that this condition is reached. For, as we have described above, the Fermi level is shifted in relation to the conduction and valence band depending on the doping type.
The result of bringing two regions, or materials of different doping state, is shown schematically in Figure 2.9. The top of the figure (a) illustrates the energy levels of the two materials prior to contact and the bottom (b) after. In order to equalise the Fermi levels, electrons (and holes) will flow from one material to another until equilibrium is reached. The effect of the resulting built in potential and energy structure will be discussed with respect to actual applications in Section 2.1.6 which will show how the p-n junction can be harnessed to create solar cells and other semiconductor devices.
Optical properties of semiconductors
Now that a general picture has been developed for the electronic structure in a semiconductor, the interaction between the material and incident electromagnetic radiation will be considered.
Optical absorption
If a photon of energy Ephoton = h f is incident on the semiconductor and Ephoton > EG, then the photon can provide an electron in the valence band with sufficient energy to enter a higher energy level - in the conduction band. This leads to a characteristic absorption profile for semiconductors called a Tauc plot. A Tauc plot maps the wavelength of incident light onto the absorption in the material. An onset of absorption is typically observed when hf ≃EG.
Direct and indirect absorption
If the conduction band minima exists at the same point in momentum space (same value of k) as the valence band edge, the material is said to be a direct band gap semiconductor. In such a scenario, the excitation of an electron from the valence to conduction band requires only the photon since momentum is inherently conserved. If the conduction band minima and valence band maxima do not coincide however, then conservation of momentum requires a phonon interaction in addition to the excitation photon. Silicon is an indirect bandgap semiconductor, whereas perovskites are mostly direct band gap semiconductors. At a basic level, the optical absorption of direct semiconductors should be greater than indirect due to only requiring a single particle interaction. The absorption can therefore take place as soon as the energy supplied to the electron from a photon is sufficient to jump across the gap. This is manifest in the requirement of only relatively thin (of the order of hundreds of nanometers) layers of GaAs or a perovskite for example. By comparison, to absorb the same quantity of light, relatively thick layers of silicon absorbers (of ∼ 1 mm thickness) are necessary.
Photoluminescence
Once excited (by absorbing a photon of sufficient energy) the electron will occupy a higher energy state within the conduction band of the semiconductor. In doing so, it will leave its own absence behind in the valence band in the form of a hole. Due to the Coulombic attraction between the negatively charged electron and the positively charged hole, the motion of the two are correlated, especially when considered in the presence of an electric field. The combined quasi-particle state of the electron and hole is known as an exciton. The extent of the interaction between the electron and hole results in excitons of different binding energies and originates from the dielectric constant of the material and thus the ability of the material to screen the interaction. In a material with a small dielectric constant, the pair is highly localised together to within a few unit cells of the material - this is known as a Frenkel exciton [31]. Conversely, if the dielectric constant of the material is high, the extent of the exciton can span several unit cells and the electron and hole become increasingly delocalised - a state known as a Wannier-Mott exciton [32].
Compared to the generation of an exciton through the absorption of a photon, photoluminescence can to some extent be considered the complete reverse process. During photoluminescence, the electron de-excites, returns to the valence band and thus recombines with the hole which it left. In doing so, the difference in energy is emitted as a photon. In addition to the radiative recombination of the electron and hole - there are two other ways in which excited charge carriers may recombine, leading to the following rate equation,
where n represents the charge carrier density, G the rate of generation of excited charge carriers and k1,k2,k3 constants. The radiative recombination mentioned above is described by the second order components of Equation 2.37. Since it necessarily involves two charge carriers, it scales quadratically with n. In an ideal semiconductor, with no defects or trap states, all recombination would occur radiatively. However, if trap states exist within the bandgap of the semiconductor, then charge carriers can relax into these states and become trapped. Once trapped, the charges could in theory escape the trap state and rejoin the bands, however this is not energetically favourable and is therefore only a minor effect. Alternatively, it will recombine with a passing charge carrier of the opposite type. Excess energy in this case is released predominantly as heat/phonons and therefore does not contribute to the more desirable radiative effect. This trap related recombination is first order in its kinetics and is described by the first order component of Equation 2.37. Finally, the third and final term in Equation 2.37 describes a three-particle process. This involves the recombination of an electron and hole, from which the energy is immediately transferred to a third interacting particle. This third particle is consequently excited to an even higher energy state, from which it will rapidly thermalise. The process is known as Auger recombination and requires extremely high charge carrier densities (in order that the three body interaction cross section can become probable).
Equation 2.37 is of course a simplified picture for an ideal semiconducting material [33]. It includes assumptions and approximations including low exciton binding energies (such that the charge carrier density is comprised predominantly free electrons and holes), and an equal number of electrons and holes (n=p). If, for example, one charge carrier type dominates over the other (n > p) then the radiative recombination term would become first order to reflect the lifetime of only the minority carrier type. The same would occur in the case of a system with a high exciton binding energy (for example, the 2D perovskites described in Section 2.2.3).
To conclude, after exciting electrons in a semiconductor via the absorption of a photon, the electron and hole will recombine again to emit a photon - photoluminescence - in an ideal scenario. However, two other effects; the trapping of charge carriers in states introduced by defects in the material and Auger recombination at high charge carrier densities can diminish how many charges actually recombine radiatively. This will be important to consider when the PL emission from the perovskites at varying levels of doping in Chapters 5 and 6 is studied.
The Burstein-Moss effect
The Burstein-Moss effect, or Burstein-Moss shift [34, 35], is a phenomenon observed in doped semiconductors in which the band gap of the material appears to shift with different concentrations of charge doping. During n-type doping, electrons populate more states close to and ultimately in the conduction band, once the density of states at the conduction band edge are fully populated. Pauli’s exclusion principle forbids more than two electrons from populating the same state [36]. Therefore, as these states begin to be filled, any optical excitation of an electron from the valence band must require more and more energy since only higher lying energy states remain available in the conduction band, with the lower ones now occupied. This is manifest in the appearance of a larger energy gap - and the optical fingerprint that comes with it, such as a blue-shift in the absorption spectrum of the material.
Applications of semiconductors
Well, after all that theoretical background I have dedicated a separate post to the applications of semiconductors - many of which we find all around us in modern life. A link to that post can be found here.